\(\require{cancel}\)
中学以降の数学では、正負の符号を省いた整数「絶対値」の概念が登場します。
計算問題や数の大小比較において、絶対値を「正負の符号(+、-)を省いた数」と扱っている方も多いのではないでしょうか。
絶対値は、中学や高校の数学のみではなく、データ分析や機械学習においても重要であり、単なる符号の有無ではなく、その概念を正確に理解することが重要です。
真剣に数学力を身に付けたいと考えているのであれば、当記事で解説する「絶対値」の本質を習得しておきましょう。
中学・高校の絶対値
絶対値の概念は、中学の数学の単元「正の数、負の数」で登場します。中学で習う概念は絶対値の初歩的な内容です。
この章で復習しましょう。
絶対値の基本的な定義
絶対値の正しい定義は、「原点からの距離」です。
原点とは、その数の中心となる点で中学の数学では「0(ゼロ)」で習うことが多いでしょう。ただし、実際の絶対値を考える場合には原点は0とは限りません。
たとえば、クラスの身長の平均値を考えてみましょう。ここでは、身長の平均を153cmと仮定します。平均値を基準値として考える場合、153cmが原点となります。
そうすると152cmの生徒は、「平均値よりも1cm低い」。154cmの生徒は、「平均値よりも1cm高い」と表現することができます。
一方で、このケースではどちらも平均値から1cm離れています。つまり、正負の符号は関わらず両者は「平均値から1cm離れている」のです。
これが、絶対値の正しい解釈です。
絶対値を「正負の符号を外した数」と考えることもできますが、これは短絡的な解釈です。今後、数学の応用も習得したいのであれば、絶対値を『原点からの距離』と正しく理解することが重要です。
ただし、単純に絶対値を用いた四則演算や大小比較では、「正負の符号を外した数」として扱っても差し支えありません。
絶対値と数直線
前節で、絶対値を「原点からの距離」と説明しました。
この考え方は数直線で表現すると理解しやすいです。下記の数直線では、原点である「0」を中心に、右側が正の整数、左側が負の整数になっています。
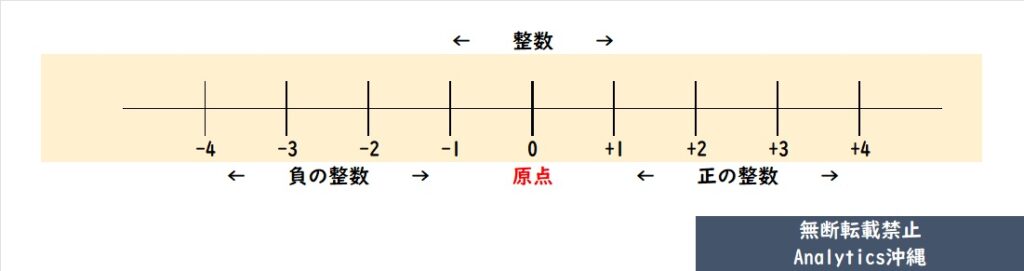
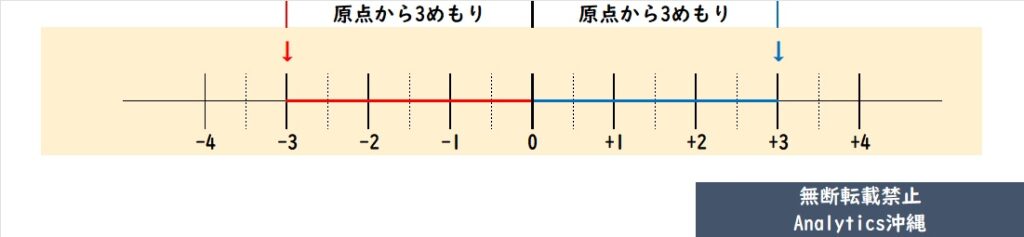
では、数直線上で「+3」と「-3」を見てみましょう。単純な数の大小で考えると「+3」が大きく、「-3」が小さいです。(-3<+3)
ただし、原点(0)からの距離という視点では、どちらも原点から3つ離れています。つまり、「+3」も「-3」も、原点からの差は3であり、これが『絶対値は等しい』と考える根拠なのです。
絶対値を用いた基本的な計算
絶対値を表す際には、”|”(縦棒)の記号を使用します。この記号は、「~の絶対値」という意味になります。
たとえば、|5|は5の絶対値を意味し、その結果は5となります。一方、|-5|は-5の絶対値を意味し、その結果も5となります。絶対値は「原点(0)からの距離」のため、正負の符号は考慮されません。
では、基本的な計算として、|-3 + 2|を考えてみましょう。まず-3と2を足して-1になり、その絶対値は1となります。このように、計算の途中で絶対値を取ることで、結果として得られる値が必ず正になることを理解しましょう。
なお、中学数学の単元「正負の数」における絶対値の学習の中心は、四則演算となります。
絶対値の四則演算の場合には、絶対値を「正負の符号を外した数」として計算するようにしましょう。
高度な数学における絶対値
絶対値は、基本的な算術から高度な数学の多岐にわたる領域まで、重要な役割を持っています。この章では、高度な数学における絶対値をいくつか紹介します。
複素数と絶対値
複素数は、実数とは異なる「虚数」領域を持っています。複素数の絶対値は、複素平面上の点と原点との間の距離として解釈できます。
この絶対値は、複素数の大きさや振幅を表すのに非常に有用です。特に、電気工学や信号処理において、複素数の絶対値は振幅を示す指標として頻繁に使用されます。
複素数zは、z=a+biと表されます(ここでa,bは実数、iは虚数単位)。
この複素数の絶対値は、 $$ \sqrt{a^2 + b^2} $$ と計算されます。
例として、z=3+4iの場合、その絶対値は∣z∣=5となります。
ベクトルの絶対値(大きさ)
ベクトルは方向と大きさの概念を持ち、その大きさは絶対値によって測定されます。物理学や工学での多くの現象はベクトルで表され、その大きさや方向が重要な役割を果たします。
ベクトルの大きさを正確に知ることで、そのベクトルが示す力や速度などの物理的な意味を理解することができます。
ベクトルvは、v=[x,y]と表されます。
このベクトルの大きさは、 $$ |v|=\sqrt{x^2 + y^2} $$ と計算されます。
例えば、ベクトルv=[3,4]の場合、その大きさは∣v∣=5です。
連続関数と絶対値
絶対値は、関数がどのように振る舞うか、特に関数が不連続になる場所を特定するのに役立つ場合があります。絶対値関数は、その性質上、不連続点を持ち得るため、この関数を研究することで、不連続性や極限のような高度な数学的概念の理解が深まります。
関数 fxは、f(x) = |x – 2 |と表されます。
この関数は、x = 2 で急な変化を示す一例です。具体的には、x = 2 より小さい値では
$$ f(x) = 2 – x $$
x = 2 より大きい値では
$$ f(x) = x – 2 $$
となります。
一般的な距離関数としての絶対値
絶対値は、最も基本的な距離の尺度として機能します。2つの点間の距離を計算する際、絶対値を使用することで、その距離が正確にどれだけ離れているのかを数値として得ることができます。
この基本的な距離概念は、より高度な距離概念やトポロジーへと拡張され、数学の多くの分野で中心的な役割を果たしています。
2つの実数 a と b の間の距離は、| a – b |で表されます。
例えば、点 a = 5 と点 b = 8 の間の距離は | a – b | です。
データ分析・機械学習における絶対値
現代のデータ分析や機械学習の分野では、絶対値の利用が頻繁に見られます。絶対値は、モデルの誤差を測定したり、データの特性を捉えるために重要な役割を持っています。
この章では、データサイエンスの領域での絶対値の具体的な使用例やその重要性について触れます。
絶対値損失と二乗損失の比較
機械学習モデルの訓練中には、モデルの予測と実際のデータとの間の差を計算するための損失関数が必要です。絶対値損失(またはL1損失)と二乗損失(L2損失)は、最もよく用いられる二つの損失関数です。
絶対値損失は、予測と実際のデータとの差の絶対値を計算します。
$$\mathrm{L}_1 = | y真実 – y予測 | $$
一方、二乗損失は、その差の二乗を計算します。
$$\mathrm{L}_2 = ( y真実 – y予測 )^2 $$
ロバスト統計における絶対値の役割
絶対値は、外れ値の影響を受けにくい、ロバストな統計的手法の基盤としても活用されます。特に中央値や絶対偏差などのロバストな統計量は、絶対値を使用して計算されることが多いです。
$$\mathrm 絶対偏差 = median(|{x}_i – median(x)│) $$
データ前処理での絶対値の利用
データの前処理ステップでは、絶対値は異常値の検出や特徴のスケーリングなど、多くのタスクで役立ちます。例えば、データの分布が歪んでいる場合、絶対値を取ることでその歪みをある程度緩和することが可能です。
機械学習モデルの正則化と絶対値
機械学習のモデルの複雑さを制限して過学習を防ぐために、正則化手法が用いられます。L1正則化は、特に絶対値を使用した正則化技法であり、モデルの重みを小さくする効果があります。
具体的には、損失関数にモデルの重みの絶対値の和を追加することで正則化を行います。
$$\mathrm 正規化項 = \lambda\Sigma|{w}_i│$$


