\(\require{cancel}\)
中学レベルの数学は「正の数・負の数」の単元から始まります。
そのため、中学数学を理解するためには、まずは正負の数を完全に理解する事が重要です。また、正負の数は今後も学習する数学の最も基本的な単元でもあり、社会生活においても必要になる知識です。
この記事では、中学レベルの数学の正の数・負の数について、数学を学び直している方や現役の学生さんに分かりやすいように解説します。
正負の数とは
わたし達が日常的に扱う「数」には、正の数と負の数があります。この章では、正負の数の基本となる概念と正負を表す符号について説明します。
正の符号
正の数とは、0より大きい数のことです。正の数は、正の符号+(プラス)で表します。
+1、+17、+32
正の数は整数のみではなく、少数も含みます。
+1.5、+17.3、+32.7
負の符号
負の数とは、0より小さい数のことです。負の数は、負の符号-(マイナス)で表します。
-1、-17、-32
負の数は整数のみではなく、少数も含みます。
-1.5、-17.3、-32.7
正の数、負の数について、0を基準に説明しました。では、0は正の数でしょうか?それとも負の数でしょうか?
答えは、そのどちらでもありません。0(零)は独特な性質を持っている数で、正負で分類することはできません。
数直線で正負の数を見る
正負の数は、数直線で表すと理解が容易になります。前章で説明した正負の数は難しい概念ではありませんので、ご理解はできたかと思うのですが、この章で、数直線で正負の数を見てみましょう。
数直線の見方
下記のように直線上に目盛りをつけて、数の大きさを表すものを数直線といいます。
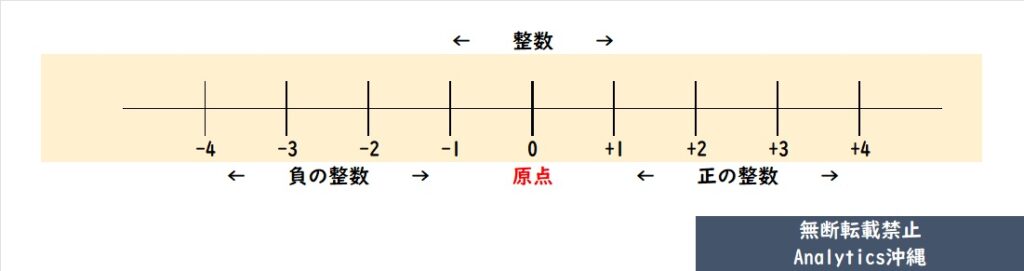
下記の赤い矢印の箇所は-2.5(負の数)、青い矢印の箇所は+2(正の数)を表しています。
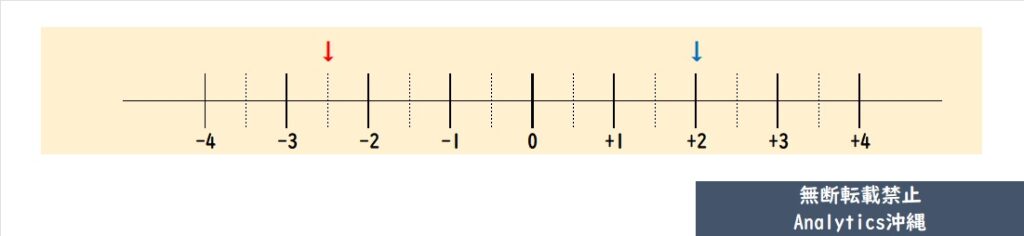
このように正負の数は数直線で表すと、視覚的にも数の大小を理解しやすくなります。
絶対値
数学を学ぶ上で「絶対値」は重要な概念になります。
絶対値とは、+や-の符号を省いた整数と説明されることもありますが、正しくは『原点からの距離』です。下記の数直線を見てみましょう。
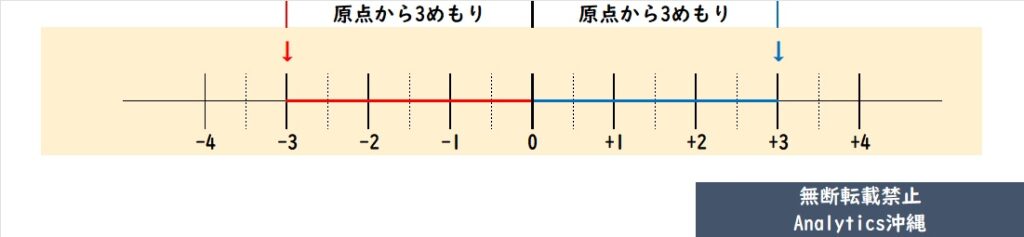
正の数+3、負の数-3ともに、原点(ゼロ)からの距離は3です。つまり、絶対値とは純粋に原点からの距離のことであり、正負による数の大きさという概念は取り除いた数のことなのです。
一見、+や-の符号を省いた整数と同様にも思えますが、それは短絡的な説明です。今後、真剣に数学を学ぶのであれば「絶対値は原点からの距離」と正しい理解をしておきましょう。
この正しい理解は、複素数やベクトルを学習する際にも有用です。
ただし、単純な数の大小比較や四則演算の際には、絶対値を+や-の符号を省いた整数と考えても構いません。
正負の数の大小を不等号で表す
2つ以上の数を並べて、数の大きさを表す不等号は小学校3年生の算数で学びます。数学が苦手な方でも、不等号の意味は理解していると思いますが、中学校の数学でも学ぶ単元のため、この章で復習してきましょう。
不等号は<,>の記号を使います。不等号の開いている箇所の数字が大きいことを表します。
大なり(>)
>は「大なり」と読みます。左の値が右よりも大きいことを意味します。
- a>bは「aはbより大きい」
- a≧bは「aはb以上」
小なり(<)
<は「小なり」と読みます。左の値が右よりも小さいことを意味します。
- a<bは「aはbより小さい」
- a≦bは「aはb以下」
3つ以上の数の大小
3つ以上の数の大小を不等号で表す場合、すべての不等号の向きを揃える必要があります。
1<3<5 または 5>3>1
加法と減法
この章では、正負の数の四則演算のうち、加法と減法について説明します。
正負の数の加法
加法とはたし算のことです。加法の結果を和といいます。
例
・(+15)+(+8)=+(15+8)=23
・(-5)+(-4)=-(5+4)=-9
例
・(-18)+(+8)=-(18-8)=-10
・(-5)+(+12)=+(12-5)=+7
加法には、加法の交換法則や結合法則という概念があります。この概念については、後日、別記事で説明します。
正負の数の減法
減法とはたし算のことです。減法の結果を差といいます。
たとえば、(+5)-(+3)の計算式で考えてみましょう。この式のひく数は、-(+3)です。そのため、-(+3)の符号を変えて、加法にして計算します。
計算の過程を下記で説明します。
例:(+5)-(+3)
- (+5)–(+3)
- (+5)+(–3)
- (+5)+(–3)=+2
例:(-6)-(-7)
- (-6)–(–7)
- (-6)+(+7)
- (-6)+(+7)=+1
加法と減法が混在した計算
ひとつの計算式で、加法と減法が混在している場合には、下記の順番で計算します。
- 減法の符号を反転させて加法のみの計算式にする
- カッコを省く
- 加法の項と減法の項に順番を変える
- 計算する
実際に、(+5)-(+2)-(-7)の計算式で考えてみましょう。計算の過程は下記の通りです。
※リスト番号は、上の概念説明の順番と一致しません。
- (+5)–(+2)–(–7)
- (+5)+(–2)+(+7)
- 5-2+7⇒5+7-2
- 5+7-2=10
乗法と除法
この章では、正負の数の四則演算のうち、乗法と除法について説明します。
正負の数の乗法
乗法とはかけ算のことです。乗算の結果を積といいます。
例
・(+8)×(+2)=+(8×2)=16
・(-6)×(-3)=-(6×3)=18
例
・(+2)×(-4)=-(2×4)=-8
・(-9)×(+5)=-(9×5)=-45
乗法には、乗法の交換法則や結合法則という概念があります。この概念については、後日、別記事で説明します。
正負の数の除法
除法とはわり算のことです。除法の結果を商といいます。
例
・(+4)÷(+2)=+(4÷2)=2
・(-15)÷(-3)=-(15÷3)=5
例
・(+49)÷(-7)=-(49÷7)=-7
・(-24)÷(+6)=-(24÷6)=-4
除法から乗法へ変更する
除法は、「わる数」を逆数にすることで、乗法にすることができます。『逆数』についての正確な解釈は別記事で紹介しますが、ここでは「分子と分母を入れ替えること」と考えてください。
例
=\(\displaystyle \frac{7}{3}\)\(\color{red}{÷\displaystyle \frac{3}{2}}\)=\(\displaystyle \frac{7}{3}\)\(\color{blue}{×\displaystyle \frac{2}{3}}\)=\(\displaystyle \frac{14}{9}\)
乗法と除法が混在した計算
ひとつの計算式で、乗法と除法が混在している場合には、下記の順番で計算します。
- 除法を逆数で反転させて乗法のみの計算式にする
- 負の符号の個数から積の符号を判断する
- 計算する
実際に、(+8)×(+3)÷(-4)の計算式で考えてみましょう。計算の過程は下記の通りです。
※リスト番号は、上の概念説明の順番と一致しません。
①= \( \displaystyle (+8) \times (+3) \color{red}{\div (-4)} \)
②= \( \displaystyle (+8) \times (+3) \color{blue}{\times \left(-\frac{1}{4}\right)} \)
③= \( \displaystyle \frac{8}{1} \times \frac{3}{1} {\times \left(-\frac{1}{4}\right)} \)
④= \( \displaystyle \frac{\cancelto{2}{8}}{1} \times \frac{3}{1} \times \left(-\frac{1}{\cancelto{1}{4}}\right) \)
⑤-6
正負の数の計算問題
下記は正負の数の計算問題(プリント)です。今記事の学習に役立てましょう。
問題
解答
近日、作成予定
